极限在大学数学中是一个很重要的内容,数学专业,非数学专业一般情况都会学习,那么今天我们就来一起看一下,数列的极限都有哪些知识点要学习,又应该怎么去了解呢?

在庄子篇中讲过这样一段话,指的是将一根木棒每天取一半,一直这样取下去,永远也取不完,这是一段很富有哲理的论述,如果我们将这些话引用到数学中,大家会发现奇妙的问题就出现了,如下所说:
《庄子·杂篇·天下》:飞鸟之景未尝动也。镞矢之疾,而有不行、不止之时。狗非犬。黄马骊牛三。白狗黑。孤驹未尝有母。一尺之棰,日取其半,万世不竭。
我们如果将最后一句话用到数学中,并且用数列的形式将其表达出来,此时你会发现木棍永远取不完,数字的排列也是永无尽头的,就会得到以下情况:

再来看一个例子:
在三世纪中期,魏晋时期的数学家刘徽创立了割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是不断倍增圆内接正多边形的边数从而求出圆周率的方法。
数学意义:“割圆术”,是以“圆内接正多边形的面积”,来无限逼近“圆面积”。
刘徽表达他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。
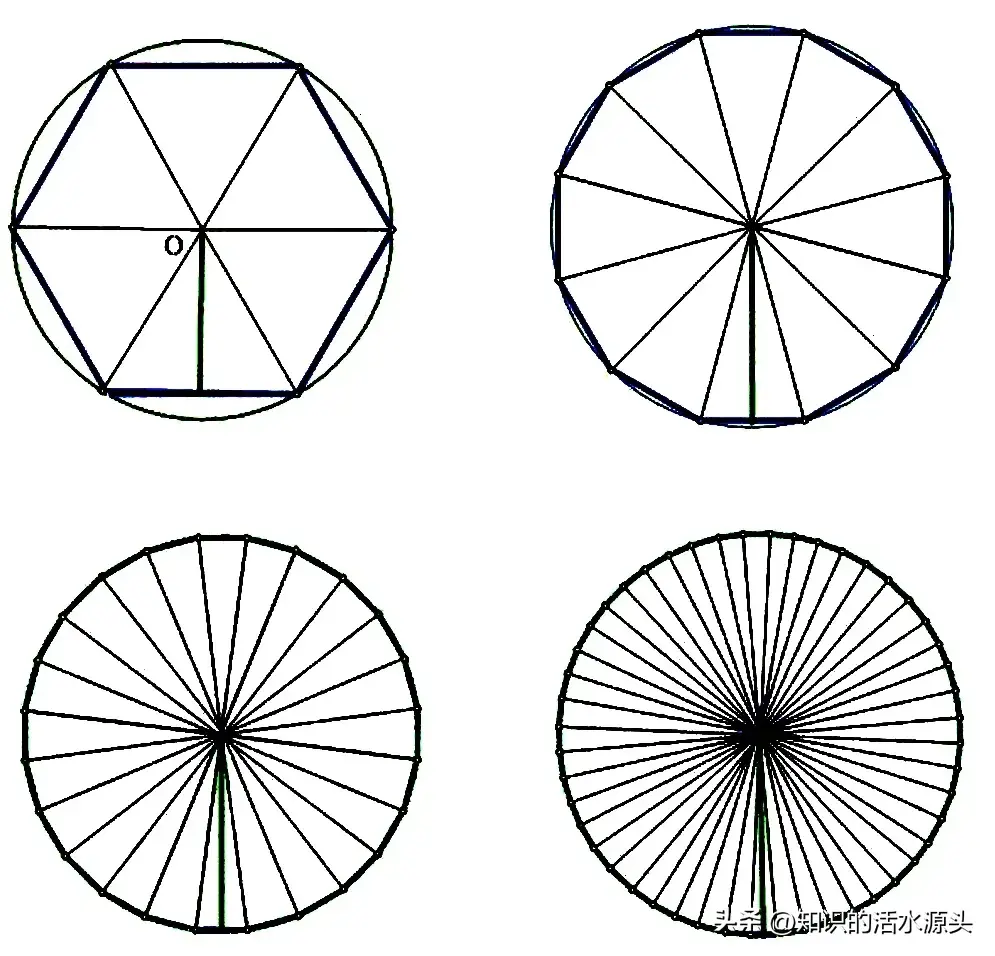
在这个割圆过程中,你会发现,随着多边形的增加,多边形的边就越逼近直线段。
接下来我们再来看一下,数列又是怎样定义的。
数列定义:按照某一法则,对每个正整数n,都有确定的实数xₙ与之对应,这列有序的数表示为:x₁,x₂,x₃,……x ₙ,……
以上的排列,我们就称为数列,其中数列的每个数,叫做数列的项,并且第n项xn称为数列的一般项或者是通项。
这样讲解,想必大家会有些模糊,我这里给大家举个例子说明一下。

注意:1、如果我们将数列的每一项看着一个动点,实际上可以在数轴上依次取x₁,x₂,x₃,…x ₙ,…
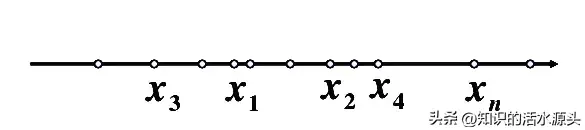
2、数列可以看为整标函数Xn=f(n),因为数列是一些分散的点,所以实质是定义在正整数集上的函数。
我们继续往下看,如果存在以下问题,那么又应该怎么解决呢?
当n无限增大时,Xn的变化趋势如何呢?
我们将n无限增大,这一变化过程可以记为n→∞
如果我们将上述(4)中的通项进行讨论,你会发现n→ ∞时,有以下结论。

我们再来看一个问题:无限接近,如果要用数学语言去刻画,应该怎么表示呢?我来给大家讲一个例子,想必大家就明白了。假设有以下数字↓
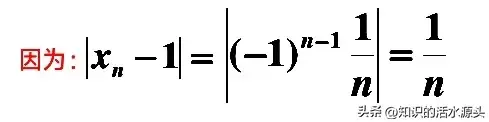
取确定数字0.01时,那么在上述条件中,就有以下关系成立↓
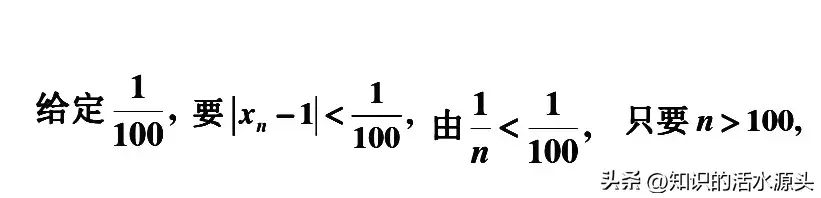
依次类推,取0.001时,就有↓

取0.0001时,也会得到同样的结论↓
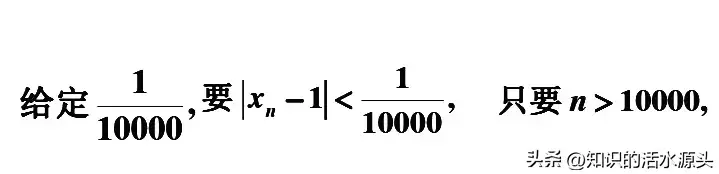
这时我们就可以得到一个总结论是成立的。
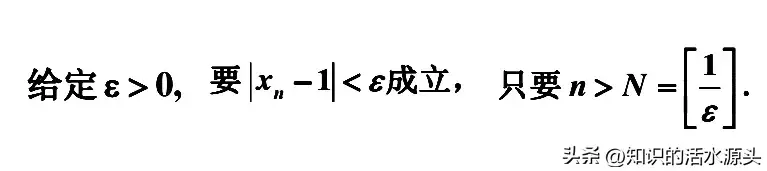
根据上述理解,我们来看一下定义到底是怎样表达呢?

注意:如果要是数列不存在极限呢?又该怎么表示,此时就可以称数列是发散的。
对于ε--N定义大家也要有一定了解。

注意:数列极限的定义未给出求极限的方法。
我们再来看一下它的几何意义是什么?我们通过数轴进行表达。
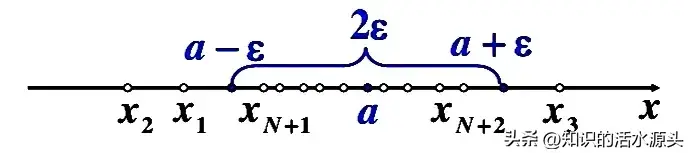
此时当n>N时,所有的点xn都落在开区间(a-ε,a+ε)内时,只有有限个(至多只有N个)点落在其外面。
通过学习,我们来看一个例题,以便大家加深理解:
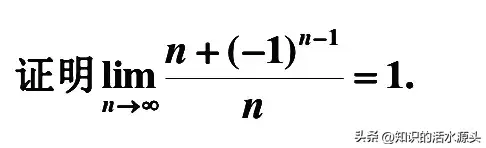
分析:该题目,是需要我们证明等式相等,大家可以借助上述定义进行证明。凑|Xn-1|
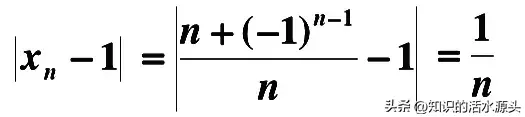
然后转换成我们所要证明的题目,最后取任意数ε>0,使得|Xn-1|<ε,只要1/n<ε,或n>1/ε,那么取N=[1/ε],则当n>N时,就有↓
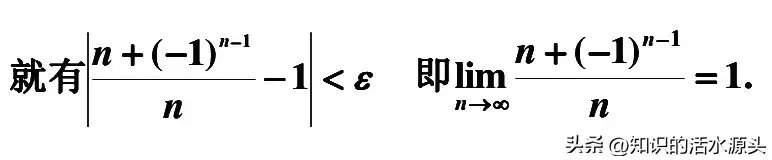
从而可得题目可证。
通过学习,大家下去过后,可以做一做以下练习题。


