
模型预测控制(Model Predictive Control,MPC)是在满足特定限制条件的前提下,控制过程的一种控制方式。
若是针对简单系统的控制,多半不需要用到复杂的MPC算法,使用PID控制器即可,如下图所示;当系统有较大的响应延迟或是高阶系统时,其控制特性会复杂到超过PID控制器可控制的程度,而MPC的模型恰恰是用来呈现复杂系统的特性。
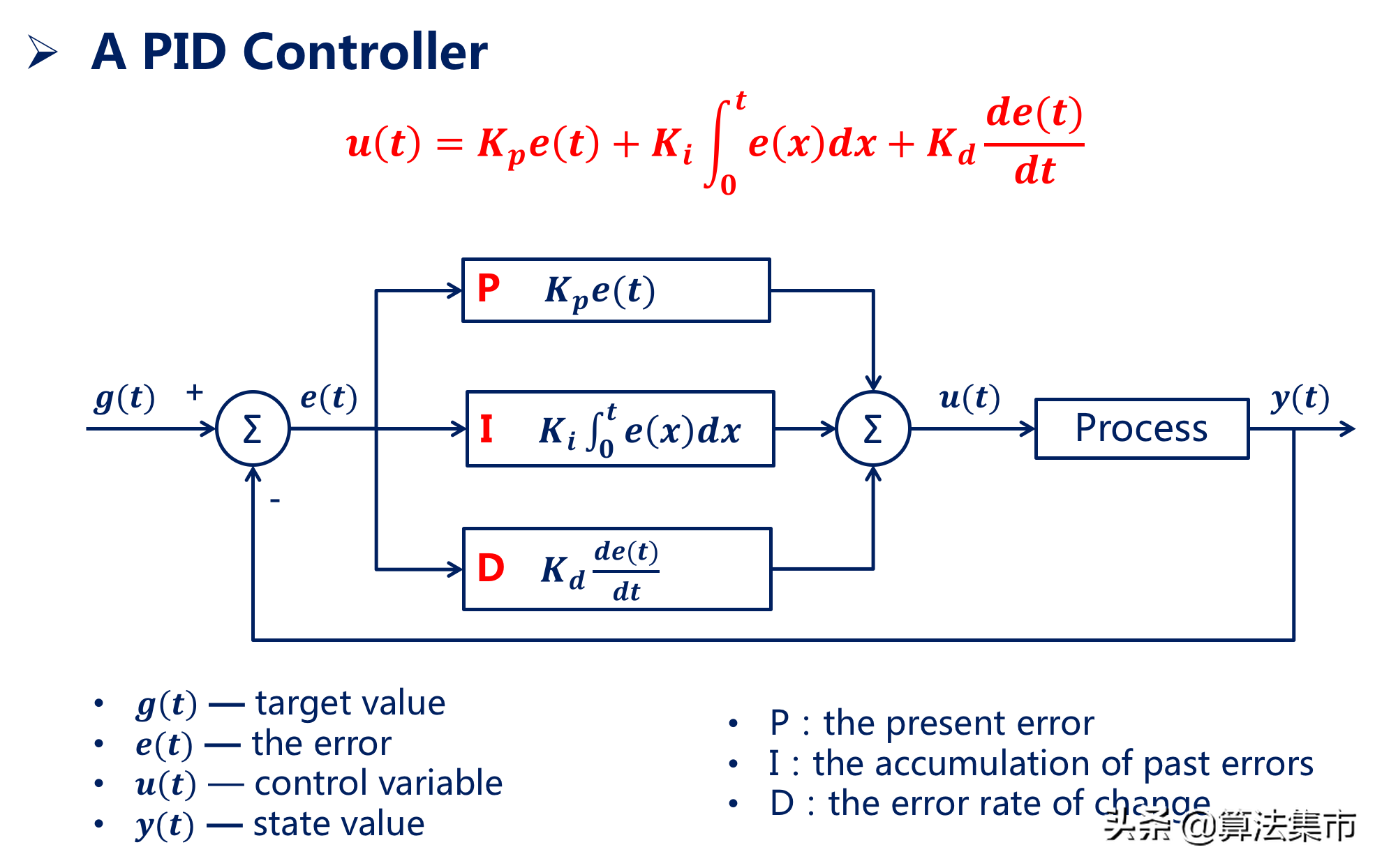
PID控制器
PID控制介绍:比例、积分、微分
为避免在刚开始学习MPC时,就陷入复杂的理论中,这里用一个骑行的小例子对MPC的基本思想进行解释。

假设我们要求骑行100公里,10小时完成。
那么有两种方案:
方案一:1小时骑行10公里,10小时完成100公里。
这个方案简单明了,但过于理想化,在具体执行过程中会遇到一些问题,比如中途需要吃饭、休息、上厕所,或有段路一直是上坡,1小时完成不了10公里;而若中途有段路一直是下坡,那1小时就可以完成20公里等等。

为解决这些突发问题,提高整个方案的可行性,提出第二种方案。
方案二:只规划未来一段时间内(比如3小时)每小时要骑行的里程,然后执行第一小时要骑行的里程,期间可能会遇到各种突发状况,每个小时过去后,要根据已经骑行的里程和剩余的里程,重新对未来3小时进行规划,同样只执行第一小时要骑行的里程。根据这样的规律,依次在新的时刻规划未来3小时要骑行的里程,并及时更正计划,最终完成骑行100公里。
可以看出,方案二在实际骑行过程中,更具有可行性,可以总结为以下三个关键步骤:
- 根据当前的体力和经验,预计未来3小时骑行的里程;
- 只规划未来3小时骑行的里程,反复进行,而非一次性规划整个骑行时间;
- 每小时结束后,根据当前状态,重新对未来3小时进行规划。
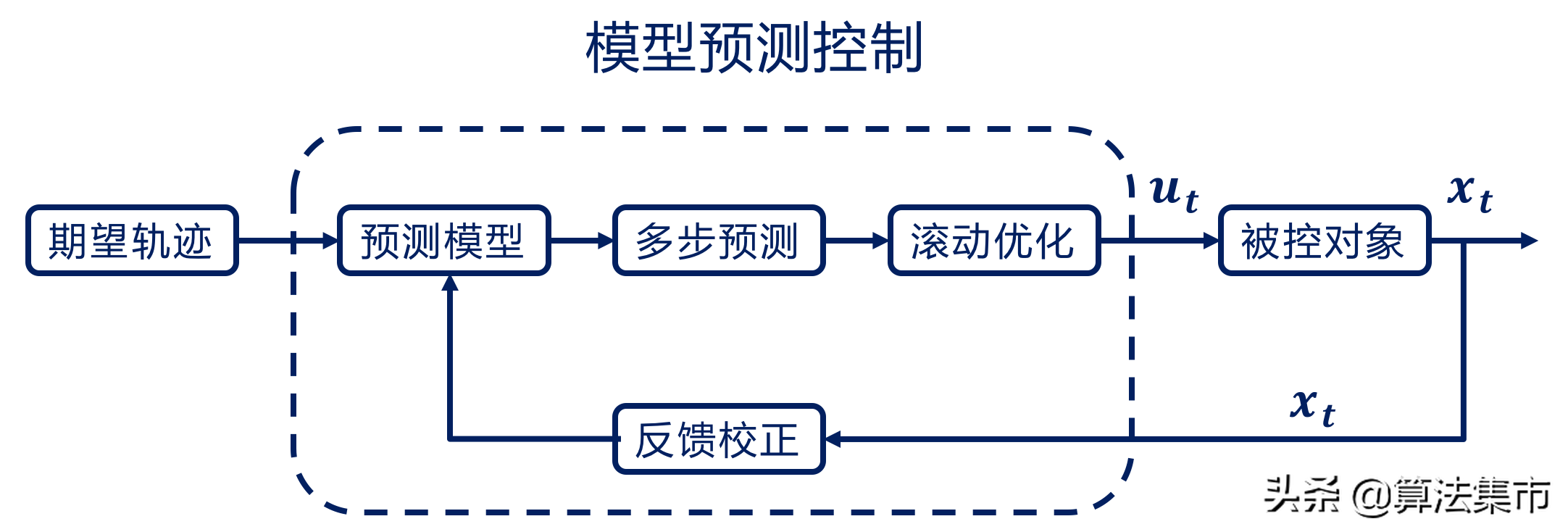
上述三个步骤,对应到MPC的实现步骤,依次为:模型预测、滚动优化和反馈校正。
- 模型预测:模型预测是MPC的基础,即根据控制系统的当前状态和预测模型,预测控制系统未来的输出。预测模型通常以状态方程的形式来表示;
- 滚动优化:MPC通过使某一性能指标的最优来求解控制量,但这个优化不是只进行一次,而是反复进行的;
- 反馈校正:为防止模型线性化或内、外部环境干扰造成控制状态的偏差,在每一新的时刻都要检测系统当前的实际状态,以此对模型预测的结果进行校正,并进行新的优化求解。
以路径跟踪为例,MPC的基本原理如下图所示。
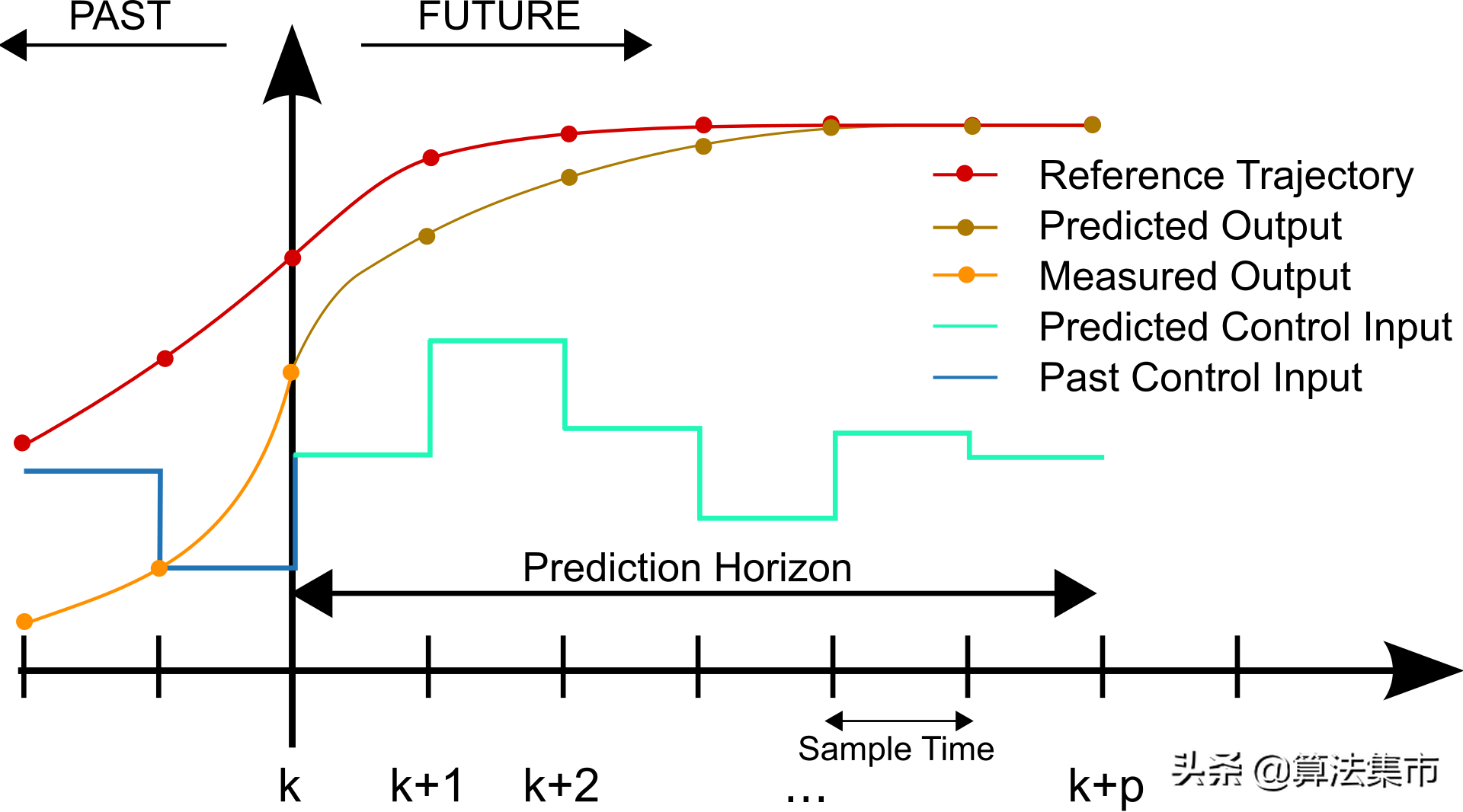
MPC路径跟踪
在路径跟踪过程中,有一条参考轨迹(reference trajectory);以时刻k作为当前时刻,控制器结合当前的状态和预测模型,预测系统未来一段时间内[k,k+p]系统的输出(predicted output);通过求解目标函数和满足约束条件的优化问题,得到一系列的控制序列(predicted control input),并将控制序列的第一个元素作为实际的控制量下发到执行器。当来到下一时刻,重复上述过程,如此滚动地完成一个个带约束的优化为题,从而实现路径的跟踪控制。
这里通过一个小例子介绍了MPC的核心内容,若要深入研究MPC,需要有相关数学基础和控制理论的知识,在实际应用中,MPC还存在着计算复杂性、控制实时性和稳定性、模型线性化、代价函数和约束设定等问题,需要我们去探索和解决。

